Binomial Heaps: Merge Better

Merge Better

The other day, I was introduced to a really cool data structure: the binomial heap. You might be familiar with binary heaps, which use a binary tree to keep items in heap order; but binomial heaps are a little more obscure. As you would expect, they too retain heap order and are often used in implementing priority queues. However, the advantage of a binomial heap is that it supports log(n) merging given two binomial heaps.

This table sums it up nicely:

In short: with a binomial heap, you earn faster merging, but give up the O(1) find-min of a binary heap.

How It Works: Binomial Trees

A binomial heap is made up of a list of binomial trees, so we’ll first discuss the latter structure, which I find to be the particularly ingenious component. A binomial tree is a recursive data structure: a tree of degree zero is just a single node and a tree of degree k is two trees of degree k-1, connected.

Thus:

• A tree of degree 1 is just two nodes, i.e., two trees of degree 0.
• A tree of degree 2 is four nodes, i.e., two trees of degree 1 (or two trees of two trees of degree zero = four nodes).
• A tree of degree 3…

Here's a visual representation:

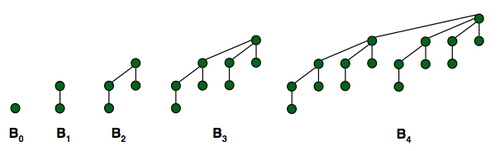
The great thing about a binomial tree is that we can merge two binomial trees of the same degree in constant time to produce a binomial tree of degree one higher! This is relatively straightforward when viewed in the context of the list above: if we have two trees of degree 2, we can just connect them and call it a tree of degree 3.

So What’s a Binomial Heap?

As stated above, a binomial heap is just a list of binomial trees. How many binomial trees, you ask? Well, assume we have n items; recall that any decimal number n can be expressed with a unique binary representation; note that a binomial tree of degree k has 2^k items; thus, for a binomial heap with n items, we can use a binomial tree of degree k for every position in n’s binary representation in which we see a 1 (rather than a 0). That was kind of verbose, so here’s an example:

If we have a heap with 13 items, we can express this in binary as 1101. This would translate to a binary tree of degree 3, a tree of degree 2, and a tree of degree 0 (with 2^3 + 2^2 + 2^0 = 8 + 4 + 1 items respectively = 13 total items).

Merging with Binomial Heaps

We can use the binary analogy to explain the Log N merge operation as well. Merging two binomial heaps is really just binary addition: for each digit i, if both heaps have a tree of degree i, then we merge them and carry-over the resulting tree of degree i + 1, carrying this process through. Since each merge is constant, and heaps of N items have at most Log N binary digits, we’re performing Log N constant-time tree merges for our heap merge—this gives us the Log N merge operation we were looking for.

Beyond merging: insert, find-min, etc.

The other operations are not too difficult to surmise. To insert, we can just merge two heaps: the original heap into which we want to insert, and a heap of a single item (the item we want to insert). Since merge is Log N, insert will be Log N as well.

Find-min is the operation in which a binomial heap loses out to a binary heap. Our heap of N items can have at most Log N binary trees. Each of these trees individually is heap-ordered, but we have no guarantee on the ordering of the trees themselves with respect to each other.

For example: we might have one tree whose root element is 5 and every element below the root is < 5; and we might have another tree whose root element is 100 and every element below the root is > 100. These are valid to have in the same heap—but we have no way of knowing which tree’s root is the minimum until we’ve assessed all Log N trees that compose the heap. Therefore, we need to look at Log N items before we can return a min.

Conclusion

This really just skims the surface of binomial heaps—there’s still delete-min, decrease-key, etc. I’m in the process of writing an OCaml implementation of the data structure, and I’ll post here when it’s completed.

By the way, the diagrams above were drawn from this presentation (Princeton CS 423), which is definitely worth looking through if you need some solid visual enforcement.